Question

According to a Los Angeles Times study of more than 1 million medical dispatches from to , the response time for medical aid varies dramatically across Los Angeles (LA Times website, November 2012). Under national standards adopted by the Los Angeles Fire Department, rescuers are supposed to arrive within six minutes to almost all medical emergencies. But the Times analysis found that in affluent hillside communities stretching from Griffith Park to Pacific Palisades, firefighters failed to hit that mark nearly of the time. The following data show the response times, in minutes, for emergency calls in the Griffith Park neighborhood.

11.8 10.3 10.7 10.6 11.5 8.3 10.5 10.9 10.7 11.2

Based on this sample of ten response times, compute the following descriptive statistics:
a. Mean, median, and mode
b. Range and standard deviation
c. Should the response time of 8.3 minutes be considered an outlier in comparison to the other response times?

Answer 1

A)Mean :10.65

Median =10.7

Mode : 10.7

B)Range = 3.5

Standard deviation :0.89916

C)The response time of 8.3 minutes should be considered an outlier in comparison to the other response times

Explanation:

A)

Data : 11.8 ,10.3, 10.7, 10.6, 11.5, 8.3, 10.5, 10.9, 10.7, 11.2

`Mean = \frac{\text{Sum of all observations}}{\text{No. of observations}}\\Mean = (11.8 +10.3+ 10.7+ 10.6+ 11.5+ 8.3+ 10.5+ 10.9+ 10.7+ 11.2)/(10)`

Mean = 10.65

Median: The mid value of the data

Data in ascending order

8.3

10.3

10.5

10.6

10.7

10.7

10.9

11.2

11.5

11.8

n=10(even)

`Median = \frac{((n)/(2))\text{th term}+((n)/(2)+1)\text{th term}}{2}\\Median = \frac{((10)/(2))\text{th term}+((10)/(2)+1)\text{th term}}{2}\\Median = (10.7+10.7)/(2)\\Median = 10.7`

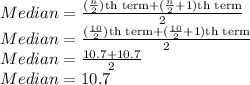
Mode : the most occurring frequency

10.7 is occurring twice while others are occurring once

So, Mode is 10.7

B) Range = Maximum - Minimum=11.8-8.3=3.5

Standard deviation :
`\sqrt{\frac{\sum(x-\bar{x})^2}{n}}`

Standard deviation :
`\sqrt{((11.8-10.65)^2+(10.3-10.65)^2+......+(10.9-10.65)^2+(10.7-10.65)^2+(11.2-10.65)^2)/(10)}`

Standard deviation :0.89916

C)

8.3

,10.3

,10.5

,10.6

,10.7

,10.7

,10.9

,11.2

,11.5

,11.8

For Q1 ( Median of lower quartile )

8.3

,10.3

,10.5

,10.6

,10.7

`Median = (n+1)/(2)\text{th term} =(5+1)/(2)=3 \text{rd term}=10.5`

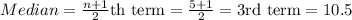
For Q3( Median of Upper quartile )

10.7

,10.9

,11.2

,11.5

,11.8

`Median = (n+1)/(2)\text{th term} =(5+1)/(2)=3 \text{rd term}=11.2`

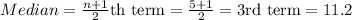
IQR = Q3-Q1=11.2-10.5=0.7

Range :(Q1-1.5IQR, Q3-1.5IQR)

Range :
`(10.5-1.5 * 0.7, 11.2-1.5 * 0.7)`

Range :(9.45, 10.15)

8.3 does not lie in this interval

So, the response time of 8.3 minutes should be considered an outlier in comparison to the other response times