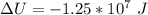Answer:
a
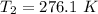
b
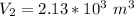
c
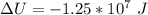
Step-by-step explanation:
From the question we are told that
The volume of the balloon is
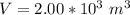
The pressure of helium is
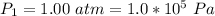
The initial temperature is
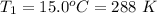
The pressure of atmosphere is
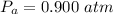
Generally the equation representing the adiabatic process is mathematically represented as
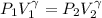
=>
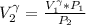
Generally
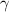 is a constant with value
is a constant with value
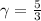 for an ideal gas
for an ideal gas
So
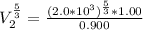
![V_2 = (\sqrt[5]{103.14641852} )^3](https://img.qammunity.org/2021/formulas/physics/college/djuaisx98oda14l7cqmp2bncf9s36ztm9m.png)
=>
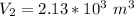
Generally the adiabatic process can also be mathematically represented as

=>
![T_2 = 288 * [(2 * 10^(3))/( 2.13 *10^(3)) ]^{ (5)/(3) -1 }](https://img.qammunity.org/2021/formulas/physics/college/8i41qgubs2cdovhrtkuwkraxgk5lrnkpy3.png)
=>
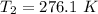
Generally the ideal gas equation is mathematically represented as
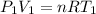
Here R is the gas constant with value
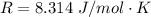
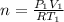
=>
![n = \frac{1.0 *10^(5) * 2.0 *10^(3)}{8.314 * 288]()
=>
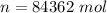
Generally change in internal energy i mathematically represented
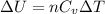
Here
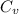 is the specific heats of gas at constant volume and the value is
is the specific heats of gas at constant volume and the value is
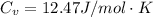
![\Delta U = 84362 * 12.47 * [T_2 - T_1 ]](https://img.qammunity.org/2021/formulas/physics/college/p1a40ug03k5cmj0xbry07bfita4tslxtni.png)
![\Delta U = 84362 * 12.47 * [276.1 - 288 ]](https://img.qammunity.org/2021/formulas/physics/college/zbrlq18il20o04231zfdihic5yw9o7ud94.png)