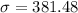Answer:
a
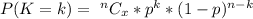
Here k is the random number of number of pairs of shoes that will be returned for refund, which can be k = 0,1 ,2,3,4 ..., 120
b
The mean is
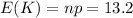
The standard deviation is
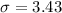
c
The mean is
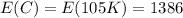
The standard deviation is
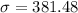
Explanation:
From the question we are told that
The cost to dealer for each refund is
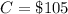
The probability that a shoe will refunded is

The number of shoes purchased is n = 120 pairs
Generally the probability distribution of the number of pairs of shoes that will be returned for refunds is
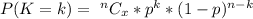
Here k is the random number of number of pairs of shoes that will be returned for refund, which can be k = 0,1 ,2,3,4 ..., 120
Generally the mean is mathematically represented as
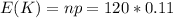
=>
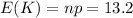
Generally the standard deviation is mathematically represented as
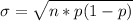
=>
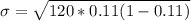
=>
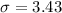
Generally the total refund cost is mathematically represented as
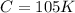
Here K denotes the number of shoes returned
Generally the mean of the total refund cost is mathematically represented as
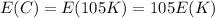
=>
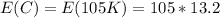
=>
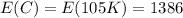
Generally the variance of the total refund cost is mathematically represented as
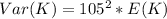
=>
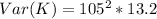
=>
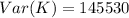
=>
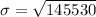
=>