Answer:
a

b
The interval means that there is 90% confidence that the true difference between the proportion of Vioxx users who suffered from heart attack and the non-Vioxx users (the placebo group ) who suffered from heart attack lie within the interval
The use of Vioxx drug should be stopped
Explanation:
From the question we are told that
The sample size for Vioxx users is

The second sample size for placebo is
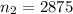
The number of Vioxx users that suffered heart attack is
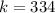
The number of non-Vioxx users that suffered heart attack is
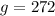
Generally the sample proportion for Vioxx users is mathematically represented as
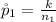
=>
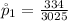
=>
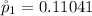
Generally the sample proportion for placebo users is mathematically represented as
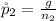
=>
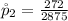
=>
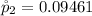
Generally the confidence level is 90% , then the level of significance is
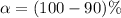
=>
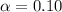
Generally the critical value of
 from the normal distribution table is
from the normal distribution table is
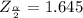
Generally the standard error is mathematically represented as
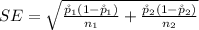
=>

=>
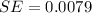
Generally the margin of error is mathematically represented as
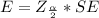
=>

=>
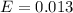
Generally the 90% confidence interval is mathematically represented as

=>

The interval means that there is 90% confidence that the true difference between the proportion of Vioxx users who suffered from heart attack and the non-Vioxx users (the placebo group ) lie within the interval
Looking at the interval we see that proportion of Vioxx users who suffered is more compared to non-Vioxx users (the placebo group )[i.e the both limit of the interval is positive ] hence the use of Vioxx drug should be stopped