Question

A box is sliding with a speed of 4.50 m/s on a horizontal surface when, at point P, it encounters a rough section. On the rough section, the coefficient of friction is not constant, but starts at 0.100 at P and increases linearly with distance past P, reaching a value of 0.600 at 12.5 m past point P.

(a) Use the work energy theorem to find how far this box slides before stopping.

(b) What is the coefficient of friction at the stopping point?

(c) How far would the box have slid iff the friciton coefficient didn't increase, but instead had the constant value of .1?

Answer 1

(a). The value of distance is 5.043 m

(b). The coefficient of friction is 0.302.

(c). The distance is 10.33 m

Step-by-step explanation:

Given that,

Speed = 4.50 m/s

Minimum friction = 0.1

Maximum friction = 0.6

Distance = 12.5 m

We know that,

The newton's second law

`F_(net)=-\mu N`

`F_(net)=-\mu mg`

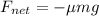
We know that,

The frictional coefficient is directly proportional to the distance.

We need to calculate the value of coefficient

Using general equation of frictional coefficient

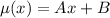`\mu(x)=Ax+B`....(I)

At x= 0,

`\mu(0)=0+B`

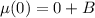
Put the value into the formula

`B=0.1`

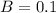
Now for value of A

Put the value in equation (I)

`0.6=A12.5+0.1`

`A=(1)/(25)`

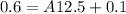
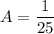
Put the value in equation (I)

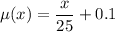`\mu(x)=(x)/(25)+0.1`......(II)

We need to calculate the work done

Using work energy theorem

`W=\int_(0)^(x){F_(net) dx}`

`W=\int_(0)^(x){-\mu_(x)mgdx}`

`W=-mg\int_(0)^(x){((x)/(25)+0.1)dx}`

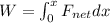
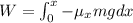
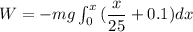
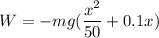`W=-mg((x^2)/(50)+0.1x)`....(III)

(a). We need to calculate the distance

Using difference of kinetic energy

`W=(1)/(2)m(v_(f)^2-v_(0)^2)`

`-mg((x^2)/(50)+0.1x)=(1)/(2)m(0-(4.50)^2)`

`(x^2)/(50)+0.1x=1.013`

`x^2+5x=50.65`

`x^2+5x-50.65=0`

`x=5.043\ m`

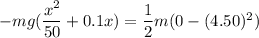
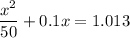
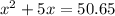
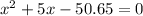
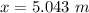
(b). We need to calculate the coefficient of friction at the stopping point

Using equation (III)

`\mu(5.043)=(5.043)/(25)+0.1`

`\mu(5.043)=0.302`

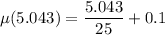
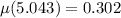
(c). We need to calculate the distance

Using formula work done

`W=-fx_(2)`

`W=-\mu mgx_(2)`

`-(1)/(2)mv_(0)^2=-\mu mgx_(2)`

`x_(2)=(v_(0)^2)/(2\mu g)`

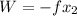
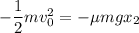
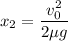
Put the value into the formula

`x_(2)=((4.5)^2)/(2*0.1*9.8)`

`x_(2)=10.33\ m`

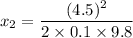
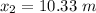
Hence, (a). The value of distance is 5.043 m

(b). The coefficient of friction is 0.302.

(c). The distance is 10.33 m