Question

A consumer has utility function U(x, y) = min{x, y}. She has $150 and the price of x and the price of y are both 1. The consumer is thinking of accepting a job in a different town, in which the price of x is 1 and the price of y is 2. Her income would remain the same. This consumer, who understands compensating and equivalent variation perfectly, is torn. While she is keen on the prospect of a move to the new town, which boasts a fine array of cultural activities for her family, she claims that, purely on the basis of her own preferences, having to move is as bad as a cut in pay of $X. She also claims she wouldn’t mind moving if when she moved she got a raise of $Y. What are the quantities $X and $Y equal to?

Answer 1

The answer is "X=50 and y=75".

Step-by-step explanation:

X = Variation equivalent

Y = Variation to compensate

Pre-movement equation:

`\to x = y = 75 \\\\ \to U= 75`

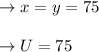
The post movement equation:

`\to x = y = 50 \\\\\to U = 50`

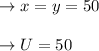
Service decline corresponds to a reduction in the salary of:

`\to 25 * 1 + 25 * 1\\\\\to 25+ 25\\\\ \to \$ 50\ \ \ _((modify \ \ Equivalent))`

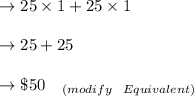
Now she wants:

`\to 25 * 1 + 25 * 2 \\\\\to 25 + 50 \\\\ \to \$ 75 \ \ \ _((compensating \ \ variation))`

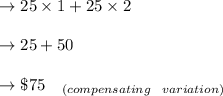
to get
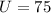`U = 75` in the new city.