Answer:
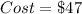
Explanation:
Given
Vertices: (−1, 5), (4, 2), and (9, −4)
Cost per foot = $8
Required
Determine the cost of fencing (-1, 5) and (4, 2)
First, we need to determine the distance between (-1, 5) and (4, 2)
Distance, d is calculated as follows:

Where
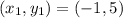

So, we have:
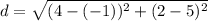
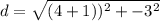
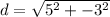


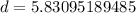
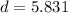 -- Approximated;
-- Approximated;
If the cost of 1 foot is $8.
5.831 feet will cost:

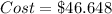
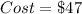 -- Approximated
-- Approximated