Given:
Jamie and Marshall's team tied Shawna and Wyatt's team for the top team score.
Marshall scores 12 less than Jamie. Shawna scored twice as much as Marshall. Wyatt scored 4 less than Shawna.
To find:
The individual score of each person.
Solution:
Let x be the score of Jamie.
Marshall scores 12 less than Jamie.
Marshall score = x-12
Shawna scored twice as much as Marshall.
Shawna score = 2(x-12)
Wyatt scored 4 less than Shawna.
Wyatt score = 2(x-12)-4
Now,
Score of Jamie and Marshall's team
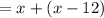
Score of Shawna and Wyatt's team
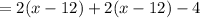
Jamie and Marshall's team tied Shawna and Wyatt's team


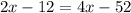
Isolate x.
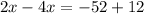
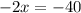
Divide both sides by -2.
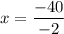

So, Jamie score = 20
Marshall score = 20-12
= 8
Shawna score = 2(20-12)
= 2(8)
= 16
Wyatt score = 2(20-12)-4
= 2(8)-4
= 16-4
= 12
Therefore, the scores of Jamie, Marshall, Shawna and Wyatt are 20, 8, 16 and 12 respectively.