Question

A person throws a pumpkin at a horizontal speed of 4.0\,\dfrac{\text m}{\text s}4.0 s m ​ 4, point, 0, start fraction, start text, m, end text, divided by, start text, s, end text, end fraction off a cliff. The pumpkin travels 9.5\,\text m9.5m9, point, 5, start text, m, end text horizontally before it hits the ground. We can ignore air resistance.

Answer 1

-27.6

Step-by-step explanation:

Khan Academy, bleh

Answer 2

d = 27.522 m

Step-by-step explanation:

The horizontal speed of a pumpkin,
`v_x=4\ m/s`

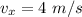
The horizontal distance covered by the pumpkin,
`d_x=9.5\ m`

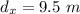
We can assume to find the the pumpkin's vertical displacement during the throw.

Firstly we can find the time of flight for the pumpkin. It can be calculated as follows :

`t=(d_x)/(v_x)\\\\t=(9.5)/(4)\\\\t=2.37\ s`

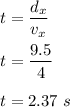
The vertical displacement during the throw is given by :

`y=u_yt+(1)/(2)a_yt^2`

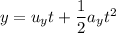
Here,
`u_y=0\ \text{and}\ a_y=-g`

So,

`y=(1)/(2)gt^2\\\\y=(1)/(2)* 9.8* (2.37)^2\\\\y=27.522\ m`

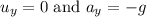
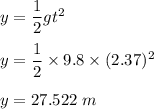
So, the vertical displacement of the pumpkin is 27.522 m.