Given:
A square corner of 16 square centimeters is removed from a square paper with an area of 9x² square centimeters.
To find:
The area of the remaining paper shape in square centimeters.
Solution:
Initial area of the square paper = 9x² sq. cm
Area of square which is removed from the initial square paper = 16 sq. cm
Subtract area of removed square from the initial area, to find the area of the remaining paper shape.
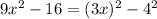
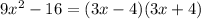
![[\because a^2-b^2=(a-b)(a+b)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/za77k2mg9bo0uop3lld48w4w0sn8py3lvq.png)
Therefore, the area of the remaining paper shape is (3x-4)(3x+4) sq. cm.
Hence, the correct option is C.