Answer:
The coordinates of
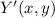 and
and
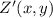 are
are
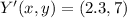 and
and
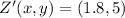 , respectively.
, respectively.
Explanation:
A translation is a geometrical operation consisting in moving a point a given distance. We proceed to describe the operation:
 (Eq. 1)
(Eq. 1)
Where:
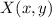 - Initial point on the cartesian plane, dimensionless.
- Initial point on the cartesian plane, dimensionless.
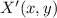 - Translated point on the cartesian plane, dimensionless.
- Translated point on the cartesian plane, dimensionless.
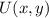 - Translation component, dimensionless.
- Translation component, dimensionless.
Vectorially speaking, we find that translation component is:
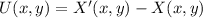
If we know that
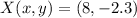 and
and
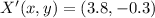 , the translation component is:
, the translation component is:
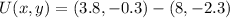
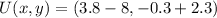
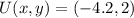
Now we determine the coordinates of
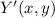 and
and
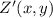 :
:
(
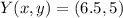 ,
,
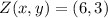 )
)
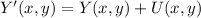 (Eq. 2)
(Eq. 2)
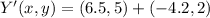
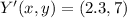
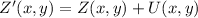 (Eq. 3)
(Eq. 3)
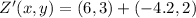
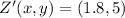
The coordinates of
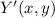 and
and
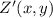 are
are
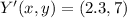 and
and
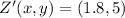 , respectively.
, respectively.