Question

Diego pays $4.50 for 3 pounds of bananas and 2 pounds of oranges. one pound of oranges cost $0.75 more than one pound of bananas let b represent the price per pound of bananas. Which equation represents the situation, and what is the price per pound of each fruit? 3b + 2b = 4.50; $0.90 per bananas, $0.90 per pound of oranges 3b + 2(0.75) = 4.50; $1.00 per bananas, $1.75 per pound of oranges 3b + 2(b + 0.75) = 4.50; $0.60 per bananas, $1.35 per pound of oranges 3b + 2b = 4.50; $1.35 per bananas, $0.60 per pound of oranges

Answer 1

Given:

Diego pays $4.50 for 3 pounds of bananas and 2 pounds of oranges.

One pound of oranges cost $0.75 more than one pound of bananas.

To find:

The equation which represents the situation, and what is the price per pound of each fruit.

Solution:

Let b represent the price per pound of bananas.

Cost of 3 pound of banana = $3b

One pound of oranges cost $0.75 more than one pound of bananas.

So, cost of one pound of oranges = $(b+0.75)

Cost of 2 pound of oranges = $2(b+0.75)

Diego pays $4.50 for 3 pounds of bananas and 2 pounds of oranges.

`3b+2(b+0.75)=4.50`

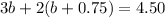
Therefore, the required equation is
`3b+2(b+0.75)=4.50`.

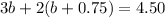On solving the above equation, we get

`3b+2b+1.50=4.50`

`5b=4.50-1.50`

`5b=3`

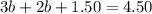
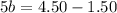
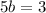
Divide both sides by 5.

`b=(3)/(5)`

`b=0.60`

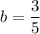
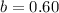
Now,

`b+0.75=0.60+0.75=1.35`

Therefore, the price of fruits are $0.60 per bananas, $1.35 per pound of oranges.

Hence, the correct option is C.