Question

Can anyone tell me why I got this wrong?

-3(x+2)>15 or x-3 ≤ -1
my answer was ( -7, 2 )

The options are
A. ( - infinity, 2)
B. (-7, -2)
C. [ - 7, infinity)
D. ( -7, 2)

Answer 1

The answer should be A.
`x \in (-\infty,\, 2)`.

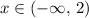Explanation:

Start with the second inequality, which is more straightforward than the first. Add
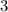`3` to both sides of this equation to separate
`x` from the numbers:

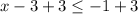`x - 3 + 3 \le -1 + 3`. The direction of the inequality sign shall stay the same.

`x \le 2`.

On the other hand, simplifying the first inequality takes a bit more work. Start by dividing both sides by
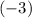`(-3)`. However, keep in mind that dividing or multiplying both sides of an inequality with a negative number will invert the direction of the inequality sign. For example, the left-hand side of an inequality might have been greater than the right-hand side. When both sides are multiplied with a number less than zero, the new left-hand side would become smaller than the new right-hand side.

Because
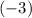`(-3)\!` is a negative number, dividing both sides of the first inequality inequality by
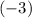`(-3)` will turn the "greater-than" sign into a "less-than" sign.

The inequality used to be:

`-3\, (x + 2) > 15`.

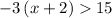After dividing both sides by the negative number
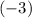`(-3)`, it becomes:

`\displaystyle ((-3)\, (x + 2 ))/((-3)) < (15)/((-3))`.

`\displaystyle (x + 2) < -5`.

`x < -7`.

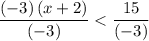The question connected the two original inequalities with "or". Therefore, the conditions will be satisfied as long as either of at least one of the two inequalities is true. Note, that
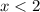`x < 2` is true whenever
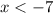`x <-7` is true. Therefore, any real number that is smaller than
`2` will meet the requirements- not just those that are smaller than
`(-7)`.

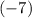The corresponding interval will be
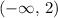`(-\infty,\, 2)`.