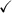Answer: see proof below
Explanation:
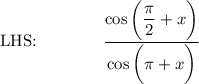
Use the Sum & Difference Identity: cos (A + B) = cos A · cos B - sin A · sin B
Recall the following from Unit Circle: cos (π/2) = 0, sin (π/2) = 1
cos (π) = -1, sin (π) = 0
Use the Quotient Identity:
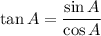
Proof LHS → RHS:
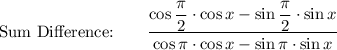
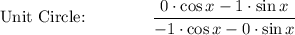
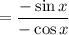
Quotient: tan x
LHS = RHS