Question

Posting one last time, please help

Answer 1

`f^(-1)(x)=√(x+1)-3`

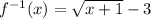
Explanation:

We have the function:

`f(x)=y=x^2+6x+8` with the domain restriction
`\{x\geq -3\}`.

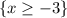And we want to find the inverse of our function.

To find the inverse of our function, we take the following steps:

• 1) Swap x and y.
• 2) Solve for y.

Therefore, our inverse will be:

`x=y^2+6y+8`

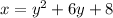
First, let's subtract 8 from both sides. So:

`x-8=y^2+6y`

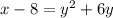
To solve for y, we can complete the square. To complete the square, we:

• 1) Divide the coefficient of the b term by 2.
• 2) Square that.
• 3) Add that number to both sides.

Our b term is 6.
`6/2=3`, and
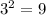`3^2=9`. So, we will add 9 to both sides. This yields:

`(x-8)+9=(y^2+6y+9)`

Simplify the left. Complete the square on the right. So:

`x+1=(y+3)^2`

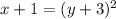
Take the square root of both sides and solve for y:

`y+3=√(x+1)\Rightarrow y=√(x+1)-3`

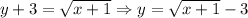
Subtract 3 from both sides. So, our inverse is:

`f^(-1)(x)=√(x+1)-3`

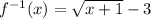
Part 2)

See below for graph.

Here is also a good time to reinforce the idea of inverses. Notice that the domain of our original function f(x) is
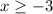`x\geq-3`. So, this means that the range of f(x) is (looking at the graph) is
`y\geq-1`.

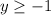When we find the inverse, we will flip the domain and range. Therefore, the domain of our inverse function will be the range of our original function, and the range of our inverse function will be the domain of our original function.

From the graph, we can see that f⁻¹(x) has a domain of
`x\geq-1` and a range of
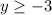`y\geq -3`. Therefore, their domain and range are indeed opposites.

And we're done!