Question

What is the slope of a line perpendicular to the line whose equation is 2x-5y=-40

Answer 1

Explanation:

Hey there!

The given equation is ; 2x - 5y = -40.

Or, 2x - 5y + 40 = 0

Slope of the equation is;

`slope(m) = ( - coeff. \: of \: x)/(coeff. \: of \: y)`

`m = ( - 2)/( - 5)`

`m = (2)/(5)`

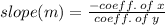
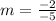
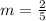
Therefore, the slope of equation is 2/5.

Now; For the perpendicular lines:

Slope of equation * slope of next line = -1

i.e M1*M2= -1

`(2)/(5) * m2 = - 1`

`2 \: m2 = - 5`

`m2 = ( - 5)/(2)`

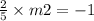
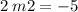
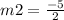
Therefore, the slope of the line which is perpendicular line to 2x - 5y + 40= 0 is -5/2.

Hope it helps....

Answer 2

`2x-5y=-40\\-5y = -40-2x\\y = (-40)/(-5)-(2x)/(-5) \\y = (2x)/(5)+8`

Slope of a line perpendicular is
`(-5)/(2)`