Question

To win the game, a placekicker must kick a football from a point 44 m (48.1184 yd) from the goal, and the ball must clear the crossbar, which is 3.05 m high. When kicked, the ball leaves the ground with a speed of 24 m/s at an angle of 31◦

from the horizontal.
The acceleration of gravity is 9.8 m/s^2.
By how much vertical distance does the ball clear the crossbar?
Answer in units of m.

Answer 1

The distance by the ball clear the crossbar is 1.15 m

Step-by-step explanation:

Given that,

Distance = 44 m

Speed = 24 m/s

Angle = 31°

Height = 3.05 m

We need to calculate the horizontal velocity

Using formula of horizontal velocity

`u_(x)=u\cos\theta`

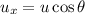
Put the value into the formula

`u_(x)=24\cos(31)`

`u_(x)=20.5\ m/s`

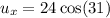
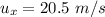
We need to calculate the vertical velocity

Using formula of vertical velocity

`u_(y)=u\sin\theta`

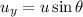
Put the value into the formula

`u_(y)=24\sin(31)`

`u_(y)=12.3\ m/s`

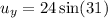
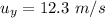
We need to calculate the time

Using formula of time

`t=(d)/(u_(x))`

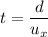
Put the value into the formula

`t=(44)/(20.5)`

`t=2.1\ sec`

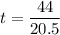
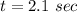
We need to calculate the vertical height

Using equation of motion

`h=u_(y)t+(1)/(2)at^2`

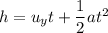
Put the value into the formula

`h=12.3*2.1-(1)/(2)*9.8*(2.1)^2`

`h=4.2\ m`

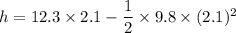
We need to calculate the distance by the ball clear the crossbar

Using formula for vertical distance

`d=h-3.05`

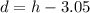
Put the value of h

`d=4.2-3.05`

`d=1.15\ m`

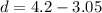
Hence, The distance by the ball clear the crossbar is 1.15 m