Question

The revenue function for a bicycle shop is given by R(x)=x⋅p(x) dollars where x is the number of units sold and p(x)=800−0.5x is the unit price. Find the maximum revenue.

Answer 1

The maximum revenue is $320,000

Explanation:

To find the maximum of a function f, the procedure is as follows:

• Find the first derivative of f.
• Equate the derivative to 0. Solve the resulting equation to get the critical points.
• Try all the critical points in the original function and select the one that maximizes it.

The revenue function for a bicycle shop is

R(x)=xp(x), where p(x)=800-0.5x. Substituting:

`R(x)=x(800-0.5x)=800x-0.5x^2`

Find the first derivative of R:

R'(x)=800-x

Equate to 0:

800-x=0

Solve:

x=800

There is only one critical point. Substitute it into the revenue function:

`R(800)=800(800)-0.5(800)^2=320,000`

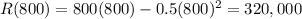
The maximum revenue is $320,000