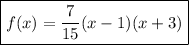Question

Writé the equation for a parabola with x-intercepts of 1 and -3 and passes through
(-9,28).

Answer 1

`\displaystyle f(x)=(7)/(15)(x-1)(x+3)`

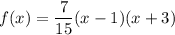
Explanation:

Equation of the Parabola

The general form of the equation of the parabola is:

`f(x)=ax^2+bx+c`

We can try to find the values of a,b, and c by using the three given points (1,0),(-3,0),(-9,28).

However, we'll use an easier method. There is another form of the parabola in case we know its roots, also called zeros or x-intercepts. If p and q are the roots of f, then f can be expressed as:

`f(x)=a(x-p)(x-q)`

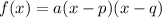
We already know the values of p=1 and q=-3, thus replacing them into the equation, we have:

`f(x)=a(x-1)(x+3)`

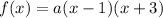
We only need to find the value of a. We do that by using the point (-9,28):

`28=a(-9-1)(-9+3)`

Operating:

`28=a(-10)(-6)=60a`

Solving for a:

`\displaystyle a=(28)/(60)=(7)/(15)`

Thus, the equation of the parabola is:

`\boxed{\displaystyle f(x)=(7)/(15)(x-1)(x+3)}`