Question

Calculate the displacement in m and velocity in m/s at the following times for a rock thrown straight down with an initial velocity of 11.4 m/s from the Verrazano Narrows bridge in New York City. The roadway of this bridge is 70.0 m above the water. (Enter the magnitudes.)

(a)
0.500 s
displacement

velocity

Answer 1

y = 6.92[m]

Vf = 16.305[m/s]

Step-by-step explanation:

To solve this problem we must use the following kinematics equations, where we must first find the final velocity.

`v_(f)=v_(i)+(g*t)`

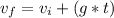
where:

Vi = initial velocity = 11.4[m/s]

Vf = final velocity [m/s]

t = time = 0.5[s]

g = gravity acceleration = 9.81[m/s^2}

Note: the positive sign in the equation above is because the acceleration of gravity goes in the direction of the motion of the rock.

Vf = 11.4 + (9.81*0.5)

Vf = 16.305 [m/s]

Now we can calculate how far the rock goes, using the following equation:

`v_(f) ^(2)= v_(i) ^(2)+(2*g*y)\\v_(f) ^(2)- v_(i)^(2) = 2*g*y\\y = (v_(f) ^(2)- v_(i)^(2))/(2*g) \\y = (16.305^(2)-11.4^(2) )/(2*9.81)\\ y=6.92[m]`

Therefore the Rock will be (70 - 6.92) = 63.07 [m] above the water level