Question

Identify the vertex
y=x^2-2x-3

Answer 1

The vertex is located at (1,-4)

Explanation:

Equation of the Quadratic Function

The vertex form of the quadratic function has the following equation:

`y=a(x-h)^2+k`

Where (h, k) is the vertex of the parabola that results when plotting the function, and a is a coefficient different from zero.

We have the following quadratic equation and we need to express it in vertex form. Thus, we need to complete the squares:

`y=x^2-2x-3`

Adding and subtracting 1:

`y=x^2-2x+1-3-1`

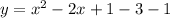
The first three terms are the square of a binomial:

`y=(x-1)^2-4`

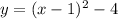
Comparing to the vertex form of a quadratic equation, the vertex is at (1,-4).

The vertex is located at (1,-4)