Answer:
Cable B will more stretch the most.
Step-by-step explanation:
Given that,
Length of material A =

Length of material B =
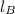
If A has a greater Young's Modulus than B.
We know that,
The deflection is defined as,
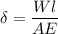
For material A,

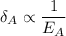
For material B,

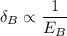
The deflection is inversely proportional to the young's modulus.
We need to find which cable will stretch the most when loaded
Using formula of deflection
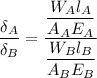
Put the value into the formula
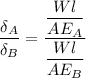
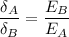
So,
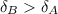
Hence, Cable B will more stretch the most.