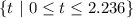Question

Physics students were modeling the height of a ball once it was dropped from the top of a 10 foot ladder. The

students found that the height, in feet, h, of the ball above the ground as a function of the number of seconds, t, since
it wasdropped was given by h(t) = 10 - 2t^2
1. Determine an appropriate domain for the given scenario. Record your domain in both interval and set builder
notation.
Interval:
Set-Builder:
Justify your reasoning for choosing the above boundaries on your domain using the context of the problem.
How would the domain for this function differ if we were looking at it outside of the context of this problem?

Answer 1

Interval notation: [0, 2.236]

Set Builder notation:
`\t\`

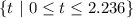
Explanation:

Given that:

Equation of height of the ball dropped from a height of 10 foot, as:

`h(t) = 10 - 2t^2`

Where
`t` is the time since the ball was dropped.

To find:

The domain of the function in Interval and set builder notation.

Solution:

Domain of a function is defined as the set of valid input values that can be given to the function for which the function is defined.

Here, input is time.

We can not have negative values for time.

Therefore, starting value for time will be 0 seconds.

And the value of height can not be lesser than that of 0 ft.

`0= 10 - 2t^2\\\Rightarrow 2t^2=10\\\Rightarrow t^2=5\\\Rightarrow t =2.236\ seconds`

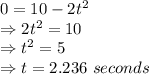
Maximum value for time can be 2.236 seconds.

Therefore the domain is:

Interval notation: [0, 2.236]

Set Builder notation:
`\t\`