Answer:
The value is

Explanation:
From the question we are told that
The sample size is n = 73
The proportion that in favor of raising the tuition is

The standard deviation is
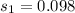
The required standard deviation
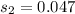
Generally the requires standard deviation is mathematically represented as
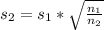
=>

=>
![(n_1)/(n_2) =[(s_2)/(s_1) ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/w7w5vhgkh5wofey3n59exipodvx34481dn.png)
=>
![(73)/(n_2) =[(0.047)/(0.098) ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/4936ku0avb7oqhp90hnv1i2mzt5m125fy7.png)
=>
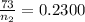
=>

=>
