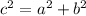Question

How are the areas of the smaller squares related to the area of the biggest square? Do you notice something?

If a = the side of one small square and b = the side of the other small square and c = the side of the biggest square, then how could you write an equation using a, b, and c with exponents?

This is the Pythagorean Theorem for all Right Triangles. ____________________

Answer 1

The sum of area of two smaller squares is equal to the area of bigger square

An equation using a, b, and c with exponents is
`c^2=a^2+b^2`

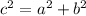
Explanation:

Let a be the side of the smallest square , b be the side of other smaller square and c be the side of biggest square

Area of square with side a =
`Side^2 = a^2`

Area of square with side b =
`Side^2 = b^2`

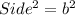
Area of square with side c =
`Side^2 = c^2`

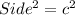
Refer the attached figure

In triangle ABC

`\angle A = 90^(\circ)`

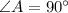
So, We can use Pythagoras theorem over here

AB = a = Base

AC = b = Perpendicular

BC = c = Hypotenuse

`Hypotenuse^2=Perpendicular^2+Base^2\\c^2=a^2+b^2`

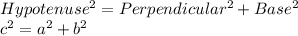
So, The sum of area of two smaller squares is equal to the area of bigger square

An equation using a, b, and c with exponents is
`c^2=a^2+b^2`