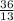Answer:
y =
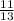 x +
x +
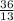
Explanation:
First, find the slope of the line passing through the points
Then find the y-intercept of the line
Then construct the formula
1. find the slope
remember the formula
 is used to find the slope
is used to find the slope
now plug in the given points
(5, 7)
(-8, -4)
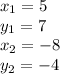
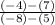
simplify and solve
=
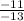
=
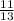
2. find the y-intercept
remember the base formula for a line
y= mx + b
where m is the slope and b is the y-intercept
we know the slope, so now plug in one of the given coordinates for a point on the line and slove to find the y-intercept
y = mx + b
y =
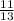 x + b
x + b
use the first set of given coordinates for a point on this line: (5, 7)
7 =
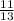 * 5 + b
* 5 + b
solve by inverse operations and simplifying
7 =
 + b
+ b
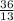 = b
= b
3. construct the formula
now we know the slope and the y-intercept, all we have to do now is substitute it into the base formula for a line:
y = mx + b
where m is the slope and B is the y-intercept
we found that
m =
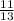
and
b =
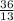
so that means the equation is
y =
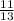 * x +
* x +