Question

Let R be a relation on a collection of sets defined as follows,

R=(A,B)

   Then pick out the correct statement(s).

1) R is reflexive and transitive

2) R is symmetric

3) R is antisymmetric.

4) R is reflexive but not transitive​

Answer 1

Options 1) and 3) are correct.

Explanation:

R=(A,B)

Reflexive:

As A⊆A,
`(A,A)`∈ R.

So, R is reflexive

Symmetric:

Let
`(A,B)`∈ R. So, A⊆B

Take
`A=\{1,2\}\,,\,B=\{1,2,3,4\}`

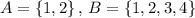
Here, A⊆B but B⊄A

So,
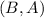`(B,A)`∉ R

R is not symmetric

Transitive:

Let
`(A,B)`∈ R and
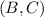`(B,C)`∈ R

So, A⊆B and B⊆C.

Therefore, A⊆C

So,

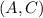`(A,C)`∈ R

Hence, R is transitive.

Option 1) is correct.

Antisymmetric:

Let (A,B)∈R and (B,A)∈R

So, A⊆B and B⊆A

Hence, A = B

So, R is antisymmetric

Option 3) is also correct.