Answer:
1) La piedra permanece en el aire en 4 segundos.
2) La piedra alcanza una distancia horizontal de 32 metros.
3) La velocidad de la piedra con la que alcanza el suelo es aproximadamente 40.792 metros por segundo.
Explanation:
El problema nos indica un caso de tipo parabólico, el cual consiste en la suma de un movimiento horizontal a velocidad y un movimiento uniforme acelerado por la gravedad desde el reposo.
1) El tiempo total que la piedra permanecería en el aire es tiempo requerido entre la parte superior del acantilado y el fondo. La ecuación cinemática que vamos a utilizar es la siguiente:
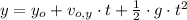 (Ec. 1)
(Ec. 1)
Donde:
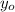 - Altura inicial, medida en metros.
- Altura inicial, medida en metros.
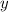 - Altura final, medida en metros.
- Altura final, medida en metros.
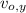 - Velocidad vertical inicial de la piedra, meadida en metros por segundo.
- Velocidad vertical inicial de la piedra, meadida en metros por segundo.
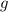 - Aceleración gravitacional, medido en metros por segundo al cuadrado.
- Aceleración gravitacional, medido en metros por segundo al cuadrado.
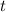 - Tiempo, medido en segundos.
- Tiempo, medido en segundos.
Si sabemos que
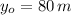 ,
,
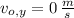 y
y
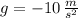 , entonces encontramos la siguiente función cuadrática:
, entonces encontramos la siguiente función cuadrática:
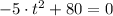 (Ec. 2)
(Ec. 2)
El tiempo en el que la piedra permanece en el aire es:
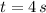
La piedra permanece en el aire en 4 segundos.
2) La distancia horizontal es descrita por la siguiente fórmula cinemática:
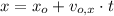 (Ec. 3)
(Ec. 3)
Donde:
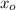 - Posición horizontal inicial, medido en metros.
- Posición horizontal inicial, medido en metros.
 - Posición horizontal final, medido en metros.
- Posición horizontal final, medido en metros.
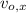 - Velocidad horizontal inicial de la piedra, medida en metros por segundo.
- Velocidad horizontal inicial de la piedra, medida en metros por segundo.
Si sabemos que
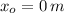 ,
,
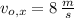 and
and
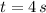 , entonces la distancia horizontal alcanzada por la piedra es:
, entonces la distancia horizontal alcanzada por la piedra es:
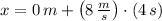
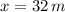
La piedra alcanza una distancia horizontal de 32 metros.
3) En primer lugar, determinamos los componentes vertical y horizontal de la velocidad final de la piedra por medio de las siguientes fórmulas cinemáticas:
Velocidad final horizontal (
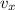 ), medida en metros por segundo.
), medida en metros por segundo.
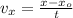 (Ec. 4)
(Ec. 4)
Velocidad final vertical (
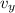 ), medida en metros por segundo.
), medida en metros por segundo.
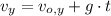 (Ec. 5)
(Ec. 5)
Si
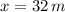 ,
,
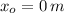 .
.
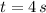 ,
,
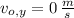 y
y
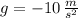 , los componentes de la velocidad final de la piedra son:
, los componentes de la velocidad final de la piedra son:
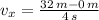
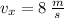
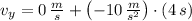
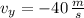
Por último, determinamos la velocidad final de la piedra por Teorema de Pitágoras:
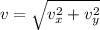 (Ec. 6)
(Ec. 6)
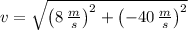
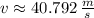
La velocidad de la piedra con la que alcanza el suelo es aproximadamente 40.792 metros por segundo.