Given that x=3sinθ-2 and y=3cosθ+4.Show that (x+2)²+ (y-4)²=9

Question

asked Mar 8, 2021 86.5k views

1 Answer

Levarne Sobotker · Answer 1 · 2021-03-12T03:35:37+0000

Answer:

First, plug-in x and y as 3sinθ-2 and 3cosθ+4 into the equation, respectively:

$((3\sin (\theta)-2)+2)^2 + ((3\cos (\theta)+4)-4)^2 = 9$

Then, +2 and -2 cancel out and +4 and -4 cancel out as well, leaving you with:

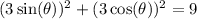
$(3\sin(\theta))^2+(3\cos(\theta))^2=9$

We can factor out 3^2 = 9 from both equations:

$9(\sin(\theta)^2+cos(\theta)^2) = 9$

We know from a trigonometric identity that
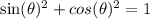$\sin(\theta)^2+cos(\theta)^2 = 1$ , meaning we can reduce the equation to:

9(1) = 9

9=9

And therefore, we have shown that (x+2)^2 + (y-4)^2 = 9, if x=3sinθ-2 and y=3cosθ+4.

Hope this helped you.