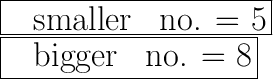
Here,We'll assume the smaller no. as x & the bigger one as y
Now,
ATQ,
(sum of two times the smaller number and three times the bigger number is 34.)
(Two times the bigger number is subtracted from the five times the smaller one)
Now,
we'll apply the elimination method to find The value of the variables↷
Here,
Let's equalize the variable ,'x'
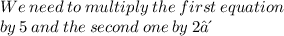
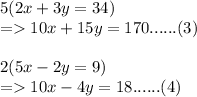
Since Now our variable'x' is equalize in Both of the equations (10x),
We'll subtract the Equation 4 From Equation 3rd so that we can find out the Value of y
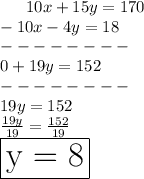
Now,
By plugging the Value of y in any of the equation,we can find the Value of x.
Here,
We'll plug the value of y into the equation 2↴
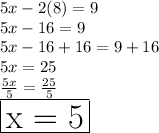
Hence, the Value of the smaller number = 5
and the value of the bigger one = 8
