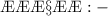
According to Newton’s second law of motion, applied force is directly proportional to the rate of change of momentum.
Momentum is basically the product of mass (m) and speed (v) of an object.
To Newton, this simply meant that if he pushes his triangular prism its speed will vary. Why speed and not mass? Because mass is constant, duh! At least that’s what everyone believed.
So far so good?
Now I ask you a question
What if I go on applying some force on an object?
Using Newton’s second law, the answer is: it’s speed goes on increasing;
which is absolutely correct!
And this result did not hurt anyone until Special Relativity came onto the main stage of Physics:
You see, the problem here is that according to Special Relativity the speed of light is the universal speed limit. No object can ever travel faster than light.
So what do we do now? We know for sure that Newton’s second law is correct.
As we know that force changes momentum: a product of mass and velocity. If velocity cannot be increased beyond “c” let’s increase the mass.
I’ll introduce something called the Lorentz factor here:
γ=11−v2c2√
applying this factor to mass:
m=m01−v2c2√
m0: is the rest mass
m = mass when the object is moving at velocity v
For v<<<c, the denominator is approximately equal to 1. However, if the speed starts getting really close to the speed of light (let's say 0.9c) the value of m gets huge.
Simply put, if the velocity increases, the object gets heavier thus making it difficult to increase its speed further.
And so, the object is never able to achieve the speed of light.
ʜᴏᴘᴇ ɪᴛ ʜᴇʟᴘꜱ❤