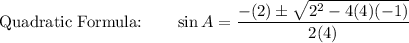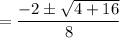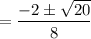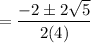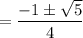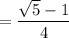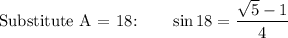Question

Please solve this question.​

Answer 1

Answer: see proof below

Explanation:

Use the Cofunction Identity: sin (90 - A) = cos (A)

Use the Double Angle Identity: sin(2A) = 2 sinA cosA

Use the Triple Angle Identity: cos (3A) = 4cos³A - 3cosA

Use the Zero Product Property: If a · b = 0, then a = 0 or b = 0

Use Pythagorean Identity: cos²A + sin²A = 1 → cos²A = 1 - sin²A

Use Quadratic Formula:
`x=(-b\pm √(b^2-4ac))/(2a)`

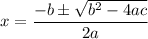
Proof LHS → RHS:

Assumption: Let A = 18°

Multiplication: then 5A = 5(18°)

→ 5A = 90°

Expand: 2A + 3A = 90°

→ 2A = 90° - 3A

Apply sin: sin (2A) = sin (90° - 3A)

Cofunction: sin (2A) = cos (3A)

Double Angle: 2 sinA cos A = cos (3A)

Triple Angle: 2 sin A cos A = 4cos³A - 3cos A

→ -4cos³A + 3cos A + 2sinA cos A = 0

Factor: cos A(-4cos² A + 3 + 2sin A) = 0

Zero Product Property: cos A = 0 or -4cos² A + 3 + 2sin A = 0

↓

Disregard (since cos A ≠ 0)

Pythagorean: -4cos² A + 3 + 2sin A = 0

→ -4(1 - sin² A) + 3 + 2sin A = 0

→ -4 + 4sin² A + 3 + 2sin A = 0

Simplify: 4sin² A + 2sin A - 1 = 0

a=4 b=2 c= -1

`\text{Quadratic Formula:}\qquad \sin A=(-(2)\pm √(2^2-4(4)(-1)))/(2(4))`

`=(-2\pm √(4+16))/(8)`

`=(-2\pm √(20))/(8)`

`=(-2\pm 2√(5))/(2(4))`

`=(-1\pm √(5))/(4)`

`=( √(5)-1)/(4)`

`\text{Substitute A = 18:}\qquad \sin 18=( √(5)-1)/(4)`