Answer: Convergent; converges to 9/5 = 1.8
======================================================
Step-by-step explanation:
The expression 8/(n^2-1) is the same as 8/( (n+1)(n-1) )
Use partial fraction decomposition to get
8/( (n+1)(n-1) ) = A/(n+1) + B/(n-1)
8 = (n+1)(n-1)*( A/(n+1) + B/(n-1) )
8 = A(n-1) + B(n+1)
8 = An-A + Bn+B
0n + 8 = (A+B)n + (-A+B)
We can see that
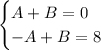
Use elimination to get 2B = 8 which leads to B = 4
Plug B = 4 into either equation of that system to solve for A getting A = -4
Therefore,
8/( (n+1)(n-1) ) = A/(n+1) + B/(n-1)
8/( (n+1)(n-1) ) = -4/(n+1) + 4/(n-1)
--------------------------------------------
Why do all this? Because it'll be helpful to set up the telescoping sum
Let's plug in a few values of n. Let's say from n = 5 to n = 10
If we do so, then we have...
-4/(5+1)+4/(5-1) = -4/6 + 4/4
-4/(6+1)+4/(6-1) = -4/7 + 4/5
-4/(7+1)+4/(7-1) = -4/8 + 4/6
-4/(8+1)+4/(8-1) = -4/9 + 4/7
-4/(9+1)+4/(9-1) = -4/10 + 4/8
-4/(10+1)+4/(10-1) = -4/11 + 4/9
I'm not evaluating or simplifying further because we'll have cancellations as shown in the diagram below. The left panel is what you see before cancelling happens, and the right hand panel is what happens after the terms pair up and cancel (since those pairs add to 0).
Note the color coding so you can see what terms pair up and cancel. The only stuff left is the 4/4 and the 4/5
So,
4/4 + 4/5 = 1 + 4/5 = 5/5+4/5 = 9/5 = 1.8
is what the infinite sum converges to. You can use a tool like wolfram alpha to confirm this answer.