Answer as a compound inequality:

Answer in interval notation: [-4, 2)
=============================================
Step-by-step explanation:
The range is the set of all possible y outputs of a function. When dealing with a graph like this, we just look at the highest and lowest points to determine which y values are possible.
The lowest point occurs when y = -4. We include this value. So far we have
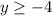 which is the same as
which is the same as
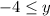
The upper ceiling for the y value is y = 2. We can't actually reach this value because of the open hole at (-3,2). So we say that

Combine
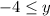 and
and
 to get the compound inequality
to get the compound inequality

This says y is between -4 and 2, including -4 but excluding 2.
To convert this to interval notation, we write [-4, 2) where the square bracket says to include the endpoint and the curved parenthesis says to exclude the endpoint.