Question

100 points!!!! Which system of equations is represented on the graph?

Answer 1

To determine the correct system of equations shown on the graph,

1. Choose any two points on the line.
2. Determine the x and y coordinates of all points
3. Determine the slope of the line
4. Determine the y-intercept of the line.
5. Plug the slope and the y-intercept in the slope intercept form.

Determining the equation of the blue line

Choosing any two points on the blue line:

• Chosen points on blue line: (0, 5) and (3, 4)

Determining the coordinates of the two points:

• y-coordinate of second point = y₂ = 4
• y-coordinate of first point = y₁ = 5
• x-coordinate of second point = x₂ = 3
• x-coordinate of first point = x₁ = 0

Determining the slope of the line:

Substitute the coordinates into the slope formula:

`\text{Slope of blue line} = (y_2 - y_1)/(x_2 - x_1)`

`\text{Slope of blue line} = (4 - 5)/(3 - 0)`

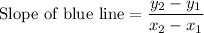
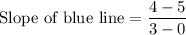
Simplify the expression as needed:

`\text{Slope of blue line} = (-1)/(3)`

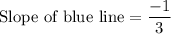
Therefore, the slope of the blue line is -1/3.

Determining the y-intercept of the line:

The point of the blue line that is intersecting the y-axis is (0, 5).

Therefore, the y-intercept of the blue line is 5.

Plug the slope and the y-intercept in the slope intercept form.

Slope intercept form: y = mx + b

[Where "m" is the slope and "b" is the y-intercept]

⇒
`y = (m)x + (b)`

⇒
`y = ((-1)/(3) )x + (5)`

⇒
`y = (-1)/(3)x + 5`

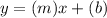
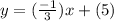
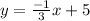
Therefore, the equation of the blue line is y = -1/3x + 5

Determining the equation of the red line:

Choosing any two points on the red line:

• Chosen points on red line: (0, -2) and (1, 0)

Determining the coordinates of the two points:

• y-coordinate of second point = y₂ = 0
• y-coordinate of first point = y₁ = -2
• x-coordinate of second point = x₂ = 1
• x-coordinate of first point = x₁ = 0

Determining the slope of the line:

Substitute the coordinates into the slope formula:

`\text{Slope of red line} = (y_2 - y_1)/(x_2 - x_1)`

`\text{Slope of red line} = (0 - (-2))/(1 - 0)`

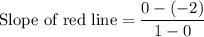
Simplify the expression as needed:

`\text{Slope of red line} = (2)/(1) = 2`

Therefore, the slope of the red line is 2.

Determining the y-intercept of the line:

The point of the red line that is intersecting the y-axis is (0, -2).

Therefore, the y-intercept of the red line is -2.

Plug the slope and the y-intercept in the slope intercept form.

Slope intercept form: y = mx + b

[Where "m" is the slope and "b" is the y-intercept]

⇒
`y = (m)x + (b)`

⇒
`y = (2 )x + (-2)`

⇒
`y = 2x - 2`

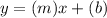
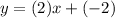
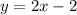
Therefore, the equation of the red line is y = 2x - 2

Final answer:

y = 2x - 2 and y = -1/3x + 5 ======> Option A