Question

find the three consecutive even intergers such that the sum of twice the smallest number and three times the largest is 42

Answer 1

6, 8, 10.

Explanation:

Let n be any integer.

Then our first even integer will be
`2n`

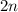
And the consecutive integers will be
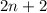`2n+2` and
`2n+4`

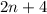
We want to find the integers such that the sum of twice the smallest number (2n) and three times the largest number (2n+4) is 42. In other words:

`2(2n)+3(2n+4)=42`

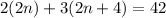
Solve for n. Distribute:

`4n+6n+12=42`

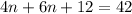
Combine like terms:

`10n+12=42`

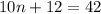
Subtract 12 from both sides:

`10n=30`

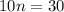
Divide both sides by 10:

`n=3`

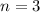
So, the value of n is 3.

This means that our first even integer is 2(3) or 6.

So, our sequence of integers is: 6, 8, 10.

And we're done!

Notes:

We use 2n because anything integer multiplied by 2 ensures that the resulting number is even. Starting out, n can be either even or odd, but by multiplying it by 2, we will get an even number.