Question

Help!
What is the answer to this question?

​

Answer 1

Its perimeter is 23 units

Explanation:

The perimeter of any figure is the sum of the lengths of its outline sides

The rule of the distance between two points is:

• 
  `d=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`

In the given figure ABCD:

Its perimeter = AB + BC + CD + DE + EA

→ Find the length of each side using the rule above

A = (-4, -2), B = (-1, 2), C = (2, 2), D = (5, -1), E = (2, -4)

→ Substitute them in the rule above to find the lengths of its sides

`AB=\sqrt{(-1--4)^(2)+(2--2)^(2)}=\sqrt{(-1+4)^(2)+(2+2)^(2)}\\\\=\sqrt{(3)^(2)+(4)^(2)}=√(9+16)=√(25)`

∴ AB = 5

`BC=\sqrt{(2--1)^(2)+(2-2)^(2)}=\sqrt{(2+1)^(2)+(0)^(2)}\\\\=\sqrt{(3)^(2)+0}=√(9+0)=√(9)`

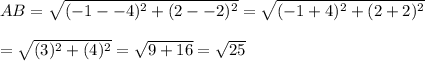
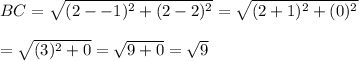
∴ BC = 3

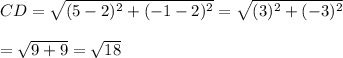
`CD=\sqrt{(5-2)^(2)+(-1-2)^(2)}=\sqrt{(3)^(2)+(-3)^(2)}\\\\=√(9+9)=√(18)`

∴ CD =
`√(18)`

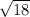
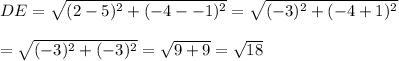
`DE=\sqrt{(2-5)^(2)+(-4--1)^(2)}=\sqrt{(-3)^(2)+(-4+1)^(2)}\\\\=\sqrt{(-3)^(2)+(-3)^(2)}=√(9+9)=√(18)`

∴ DE =
`√(18)`

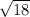
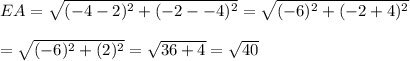
`EA=\sqrt{(-4-2)^(2)+(-2--4)^(2)}=\sqrt{(-6)^(2)+(-2+4)^(2)}\\\\=\sqrt{(-6)^(2)+(2)^(2)}=√(36+4)=√(40)`

∴ EA =
`√(40)`

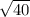
→ Add them to find the perimeter of the figure ABCDE

∴ Its perimeter = 5 + 3 +
`√(18)` +
`√(18)` +
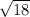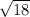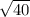`√(40)` ≅ 22.8098

→ Round it to the whole number

∴ Its perimeter = 23 units