Answer:
The other endpoint is (-33, 17)
Explanation:
The rule of the mid-point of a segment whose endpoints are
(
 ,
,
 ) and (
) and (
 ,
,
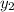 ) is
) is
In our question
∵ The coordinates of the endpoints of a segment are (-15, 13) and (x, y)
∴
 = -15 and
= -15 and
 = x
= x
∴
 = 13 and
= 13 and
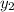 = y
= y
∵ The coordinates of the mid-point of this segment are (-24, 15)
∴
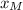 = -24 and
= -24 and
 = 15
= 15
→ Use the rule of the mid-point to find x and y
∵

→ Multiply both sides by 2
∴ -48 = -15 + x
→ Add 15 to both sides
∴ -33 = x
∵

→ Multiply both sides by 2
∴ 30 = 13 + y
→ Subtract 13 from both sides
∴ 17 = y
∴ The other endpoint is (-33, 17)