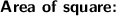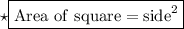What we get to know by looking at picture :
- There are two figures: 1. square 2. circle inside it touching all square's wall.
- As O is center of circle (given) ∴ OP is radius of circle
- As the sides are of square , therefore AB = BC = DC = AD

To find :

Given:
- O is the center of the circle.
- ABCD is square
- Length of BC is equal to 6.84.

Concept:
So as we can orange doesn't lies inside circle. And the wall of circle touches all four sides of circle. So first we have to find area of circle and then Area of square. And then we will subtract the ares. The result will be Area of orange part.

Solution:


To find area of circle we need radius of it i.e Length of OP.
As BC = AB
∴AB = 6.84
As O is the center of square ∴it's center of circle too
Therefore:

Now Let's find area :


here :
- r is the radius of circle.