Question

1. In ABC, A=45 degrees, B=75 degrees, and BC=12. What is the length of AB?

Answer 1

We know that sum of the interior angles of any triangle equal 180° :

So :

A + B + C = 180°

45° + 75° + C = 180°

120° + C = 180°

Both sides minus ( 120°) :

C = 180° - 120°

C = 60°

_________________________________

According to the theorem of sinuses :

`(AB)/( \sin(C) ) = (BC)/( \sin(A) ) \\`

`(AB)/( \sin(60) ) = (12)/( \sin(45) ) \\`

`(AB)/( ( √(3) )/(2) ) = (12)/( ( √(2) )/(2) ) \\`

`Multiply \: both \: sides \: by \: ( √(3) )/(2)`

`AB = (24)/( √(2) ) * ( √(3) )/(2) \\`

`AB = (12 √(3) )/( √(2) ) \\`

`AB = (2 * 6 √(3) )/( √(2) ) \\`

`AB = \frac{ ({ √(2) })^(2) * 6 √(3) }{ √(2) } \\`

`AB = ( √(2) * √(2) * 6 √(3) )/( √(2) ) \\`

`AB = ( √(2) * 6 √(3) )/(1) \\`

`AB = √(2) * 6 √(3)`

`AB = 6 √(2 * 3)`

`AB = 6 √(6)`

_________________________________

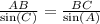
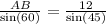
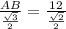
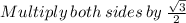
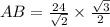
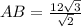
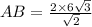
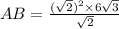
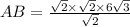
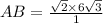
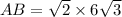
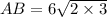
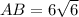
I think this is the correct answer.

And we're done.

Thanks for watching buddy good luck.

♥️♥️♥️♥️♥️