We know that the square of any number is greater than or equal to zero ;
So if have a number like x :
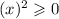
_________________________________
Now we have a number which is
( a - b ) ;
So we have :
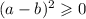
##############################
Reminder :
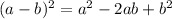
##############################
So we have :
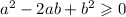
Both sides plus 2ab :
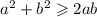
Divided both sides by 2 :
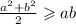
_________________________________
And we're done.
Thanks for watching buddy good luck.
♥️♥️♥️♥️♥️