Question

A man starts walking at a steady speed of 1 m/s and 6s later his son sets off from the same point in pursuit of him, starting at rest and accelerating at 2/3 m/s/s. How far do they go before they are together?

Answer 1

The father will walk 6 more meters and the son will walk 12 meters

Step-by-step explanation:

Uniform Speed and Acceleration

This is a problem where two objects have different types of motion. The father walks at a constant speed and later, his son starts a constant acceleration motion in pursuit of him.

Let's start with the father, whose speed is v=1 m/s during t=6 seconds. He travels a distance:

`x=vt=1*6=6\ m`

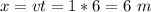
Now the son, starting from rest (vo=0) accelerates at a=2/3 m/s^2. His speed will increase and eventually, he will catch up with his father. Let's suppose it happens at a time t1.

The distance traveled by the son is given by:

`\displaystyle xs=v_o.t_1+(a.t_1^2)/(2)`

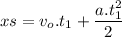
Since vo=0:

`\displaystyle xs=(a.t_1^2)/(2)`

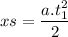
The father will continue with constant speed and travels a distance of:

`xf=v.t_1`

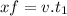
For them to catch up, the distance of the son must be 6 m more than the distance of the father, because of the leading distance he has already taken. Thus:

`xs=xf+6`

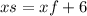
Substituting the equations of each man:

`\displaystyle (a.t_1^2)/(2)=v.t_1+6`

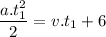
We know a=2/3, v=1:

`\displaystyle (2)/(3)\cdot(t_1^2)/(2)=t_1+6`

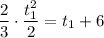
Simplifying:

`\displaystyle (t_1^2)/(3)=t_1+6`

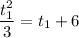
Multiply by 3:

`t_1^2=3t_1+18`

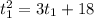
Rearranging:

`t_1^2-3t_1-18=0`

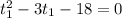
Factoring:

`(t_1-6)(t_1+3)=0`

Solving:

`t_1=6 , t_1=-3`

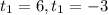
Since time cannot be negative, the only valid solution is

`t_1=6\ s`

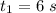
The distance traveled by the son in 6 seconds is:

`\displaystyle xs=(2/3\cdot 6^2)/(2)`

`xs=12\ m`

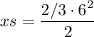
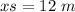
Note the father will travel

`xf=1*6=6\ m`

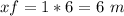
This 6 m plus the 6 m he was ahead of the son, make them meet while walking at 6 seconds.

Answer: The father will walk 6 more meters and the son will walk 12 meters