To find:-
- To find the electric field due to a point charge using Gauss's Law .
Answer:-
Gauss's law in electrostatics states that the electric flux through a closed surface is equal to 1/ε0 times the charge enclosed by that surface, that is,
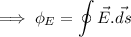
Also ,
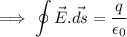
Linear density of charge:-
It ise defined as charge per unit length. Mathematically,
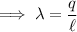
where ,
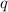 is the charge .
is the charge .
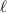 is the length of the conductor.
is the length of the conductor.
For figure see attachment.
Now let us assume that the linear density of charge is
 . There is a point P near the wire at a distance of " r " from it , where we are interested in calculating the electrical field. Imagine a coaxial Gaussian cylinder of length
. There is a point P near the wire at a distance of " r " from it , where we are interested in calculating the electrical field. Imagine a coaxial Gaussian cylinder of length
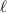 , and radius " r " such that the point P lines on its surface.
, and radius " r " such that the point P lines on its surface.
Calculating Electrical flux through the cylinder:-
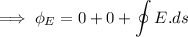
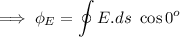
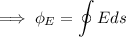
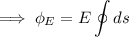
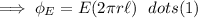
From Gauss's law:-


Therefore , from equation (1) and (2) , we have;


And we are done!