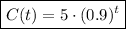Question

1. Contaminated water is subjected to a cleaning process. The concentration of the pollutants is initially 5 mg per liter of water. If the cleaning process can reduce the pollutant by 10% each hour, define a function that can represent the concentration of pollutants in the water in terms of the number of hours that the cleaning process has taken place.​

Answer 1

`C(t)=5\cdot(0.9)^t`

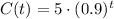
Explanation:

The exponential function is often used to model natural growing or decaying processes, where the change is proportional to the actual quantity.

An exponential decaying function is expressed as:

`C(t)=C_o\cdot(1-r)^t`

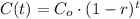
Where:

C(t) is the actual value of the function at time t

Co is the initial value of C at t=0

r is the decaying rate, expressed in decimal

The concentration of the pollutants starts at Co=5 mg/lt. We also know the pollutant reduces its concentration by 10% each hour. This gives us a value of r = 10% / 100 = 0.1

Substituting into the general equation:

`C(t)=5\cdot(1-0.1)^t`

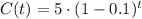
Operating:

`\boxed{C(t)=5\cdot(0.9)^t}`