Question

In 154 N38 what digit should be replaced to N to make the number divisible by 3,6 and 9?​

Answer 1

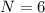`N = 6` so that number becomes divisible by 3, 6 and 9.

Explanation:

In Number Theory there is a rule of thumb which states that sum of digits of a multiple of 3 equal 3 or a multiple of three. If we know that
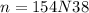`n = 154N38`, then its sum of digits is:

`x = 1 + 5+4+N+3+8`

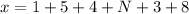
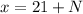`x = 21+N` (Eq. 1)

We have to determine which digits corresponds to multiples of three, there are four digits:

N = 0

`x = 21+0`

`x = 21` (
`3* 7 = 21`)

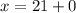
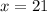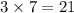N = 3

`x = 21+3`

`x = 24` (
`3* 8 = 24`)

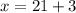
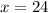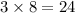N = 6

`x = 21+6`

`x = 27` (
`3* 9 = 27`)

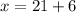
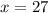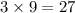N = 9

`x = 21+9`

`x = 30` (
`3* 10 = 30`)

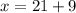
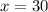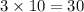We get the following four distinct options: 154038, 154338, 154638, 154938. Now we find which number is divisible by 6 and 9 by factor decomposition:

`154038 = 2* 3* 25673`

`154338 =2* 3* 29 * 887`

`154638 = 2* 3* 3* 11* 11* 71`

`154938 = 2* 3* 7* 7* 17* 31`

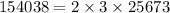
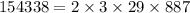
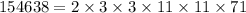
It is quite evident that
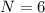`N = 6` so that number becomes divisible by 3, 6 and 9.