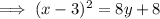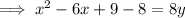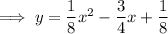Answer:
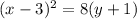
Explanation:
Standard form of a parabola with a vertical axis of symmetry:


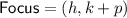
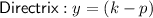

If p > 0, the parabola opens upwards, and if p < 0, the parabola opens downwards.
From inspection of the graph:
- Vertex = (3, -1)
- Directrix = y = -3
Therefore:
Use the Directrix equation to find p
⇒ y = (k - p)
⇒ -3 = -1 - p
⇒ p = 2
Therefore the equation of the conic section is:
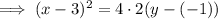
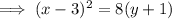
Rearranging in standard form
 :
: