Question

Two part-time instructors are hired by the Department of Statistics and each is assigned at random to teach a single course in probability, inference, or statistical computing. Assume that more than one section of each course is offered. List the outcomes in the sample space [Hint: each element consists of a pair of assignments]. Find the probability that they will teach different courses. Note: carefully define your notation (e.g. any events) in words before solving the problem.

Answer 1

The probability that they will teach different courses is
`(2)/(3)`.

Explanation:

Sample space is a set of all possible outcomes of an experiment.

In this case we will write the sample space in the form (x, y).

Here x represents the course taught by the first part-time instructor and y represents the course taught by the second part-time instructor.

Denote every course by their first letter.

The sample space is as follows:

S = {(P, P), (P, I), (P, S), (I, P), (I, I), (I, S), (S, P), (S, I) and (S, S)}

The outcomes where the the instructors will teach different courses are:

s = {(P, I), (P, S), (I, P),(I, S), (S, P) and (S, I)}

The probability of an events E is the ratio of the number of favorable outcomes to the total number of outcomes.

`P(E)=(n(E))/(N)`

Compute the probability that they will teach different courses as follows:

`P(\text{Different courses})=(n(s))/(n(S))=(6)/(9)=(2)/(3)`

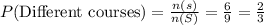
Thus, the probability that they will teach different courses is
`(2)/(3)`.