Question

An airplane is traveling at 250 m/s in level flight. If the airplane is to make a change in direction, it must travel is a horizontal curved path. To fly in the curved path, the pilot banks the airplane at an angle such that the lift has a horizontal component that provides the horizontal centripetal acceleration to move in a horizontal circular path. If the airplane is banked at an angle of 15.0 degrees, then the radius of curvature of the curved path of the airplane is

Answer 1

The radius of curvature of the curved path of the airplane is 23784.356 meters (23.784 kilometers).

Step-by-step explanation:

We assume that airplane can be represented as a particle. The free body diagram of the vehicle is presented below as attachment, whose variables are:

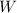`W` - Weight of the airplane, measured in newtons.

`F` - Lift, measured in newtons.

`\theta` - Banking angle, measured in sexagesimal degrees.

The equations of equilibrium associated with the airplane are, respectively:

`\Sigma F_(r) = F\cdot \sin \theta = m\cdot (v^(2))/(R)` (Eq. 1)

`\Sigma F_(z) = F\cdot \cos \theta - W = 0` (Eq. 2)

From (Eq. 2):

`F = (W)/(\cos \theta)`

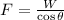
In (Eq. 1):

`W\cdot \tan \theta = m\cdot (v^(2))/(R)`

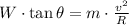
By using the definition of weight, we eliminate the mass of the airplane:

`g\cdot \tan \theta = (v^(2))/(R)`

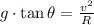
Where:

`g` - Gravitational acceleration, measured in meters per square second.

`v` - Speed, measured in meters per second.

`R` - Radius of curvature, measured in meters.

Lastly, we clear the radius of curvature with the expression:

`R = (v^(2))/(g\cdot \tan \theta)`

If we know that
`v = 250\,(m)/(s)`,
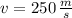`g = 9.807\,(m)/(s^(2))` and
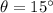`\theta = 15^(\circ)`, the radius of curvature is:

`R = (\left(250\,(m)/(s) \right)^(2))/(\left(9.807\,(m)/(s^(2)) \right)\cdot \tan 15^(\circ))`

`R = 23784.356\,m`

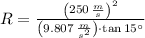
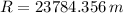
The radius of curvature of the curved path of the airplane is 23784.356 meters (23.784 kilometers).