Question

The Doe family had a rectangular garden with a 58-foot perimeter. They reduced the length by 7 feet and decreased the width to be half as wide as it was originally. This resulted in a garden with a 34-foot perimeter. What is the area of the new smaller garden?

Answer 1

60 square foot

Explanation:

Perimeter of a rectangular garden = 58 foot

Let x and y denote length and width of the rectangular garden.

2 (Length + Width) = Perimeter of the rectangular garden

`2(x+y)=58\\x+y=(58)/(2)\\ x+y=29`

So,

length = x

width = y =
`29-x`

The length is reduced by 7 feet and the width becomes half.

New length =
`x-7`

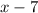
New width =
`(1)/(2)(29-x)`

New perimeter = 34 foot

`2[(x-7)+(1)/(2)(29-x)]=34\\ 2[2(x-7)+(29-x)]=2(34)\\2(x-7)+(29-x)=34\\2x-14+29-x=34\\2x-x-14+29=34\\x+15=34\\x=34-15\\x=19`

So,

New length
`=x-7=19-7=12\,\,foot`

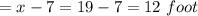
New width =
`(1)/(2)(29-19)=(1)/(2)(10)=5\,\,foot`

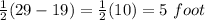
Area of the new smaller garden = New length × New Width

= 12 × 5

= 60 square foot