Question

Given: △ABC, m∠A=60°

m∠C=45°, AB = 9
Find: Perimeter of △ABC
Area of △ABC
Please don't use trig

Answer 1

Perimeter of ΔABC =32.31 units

Area of the triangle ABC = 47.81 sq. unit

Explanation:

In triangle ABC

`\angle A = 60^(\circ)\\\angle C = 45^(\circ)`

Angle sum property of triangle : The sum of the measures of the all angles of triangle is 180°

`\angle A + \angle B + \angle C = 180^(\circ)\\60 + \angle B + 45 = 180\\\angle B + 105 = 180\\\angle B = 75^(\circ)`

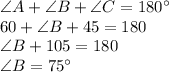
Now we are supposed to find the perimeter and the area of the ΔABC

We will use the sine rule to find the lengths of sides BC and AC

Sine rule :
`(Sin A)/(BC)=(Sin B)/(AC)=(Sin C)/(AB)`

`(Sin 60)/(BC)=(Sin 75)/(AC)=(Sin 45)/(9)\\BC * sin(45) = 9 * sin(60)\\ BC = 11.02`

`AC * sin(45) = 9 * sin(75)`

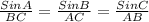
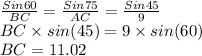
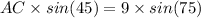
AC = 12.29

Perimeter of ΔABC = AB + BC + AC

Perimeter of ΔABC = 9 + 11.02 + 12.29 =32.31 units

Area by using the sine rule:

Area of the triangle ABC =
`(1)/(2) (AB)(BC) sin B`

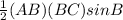
Area of the triangle ABC =
`(1)/(2) (9)(11) sin(75)`

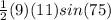
Area of the triangle ABC = 47.81 sq. unit